Details

Let be n an integer prime with 10 e.g. 7.

1/7 = 0.142857 142857 142857 ....

We see that the decimal part has a cycle: 142857. The length of this cycle is 6. In the same way:

1/11 = 0.09 09 09 .... Cycle length is 2.

Task

Given an integer n (n > 1), the function cycle(n) returns the length of the cycle if n and 10 are coprimes, otherwise returns -1.

Exemples:

cycle(5) = -1
cycle(13) = 6 -> 0.076923 076923 0769
cycle(21) = 6 -> 0.047619 047619 0476
cycle(27) = 3 -> 0.037 037 037 037 0370
cycle(33) = 2 -> 0.03 03 03 03 03 03 03 03
cycle(37) = 3 -> 0.027 027 027 027 027 0
cycle(94) = -1 

cycle(22) = -1 since 1/22 ~ 0.0 45 45 45 45 ...

Note

• Translators are welcome for all languages.

My Solution

import math
import fractions

def cycle(n) :
    if n==2 or n==5 :
        return -1
    t = phi(n)
    p = primes(t)
    divisor = []
    for i in p:
        x = i
        while t % i == 0:
            divisor.append(i)
            t //= i
        if isprime(t):
            divisor.append(t)
            break
    divisor.sort()
    print(divisor)
    for i in divisor:
        if 10**i % n == 1:
            break
    return i

def phi(n):
    '''compute Euler's totient function values.'''
    amount = 0
    for k in range(1, n + 1):
        if math.gcd(n, k) == 1:
            amount += 1
    return amount


def isprime(n):
    """Returns True if n is prime."""
    if n == 2:
        return True
    if n == 3:
        return True
    if n % 2 == 0:
        return False
    if n % 3 == 0:
        return False
    i = 5
    w = 2
    while i * i <= n:
        if n % i == 0:
            return False
        i += w
        w = 6 - w
    return True

def primes(limit):
    D = {}
    q = 2
    while q <= limit:
        if q not in D:
            yield q
            D[q * q] = [q]
        else:
            for p in D[q]:
                D.setdefault(p + q, []).append(p)
            del D[q]
        q += 1

print(cycle(219199))

这道题是求 $1/n$ 的循环小数位数的。通过观察其实可以得到如下的性质，假设 $1/n$ 的循环小数位数有 $p$ 位，则有：

10**p % n == 1

其实也很好理解，就是 10 扩大 $p$ 倍，小数点向右移动 $p$ 位，整数部分恰好位一个循环数，小数部分则等于 $1/n$ 。

但是如果按照这个思路来进行求解，写一个循环，对一个稍微大一点的数，如上面的 219199，它的循环位数是 36180。暴力写循环根本就行不通！

Other Solutions

lechevalier

def cycle(n):
    if not n % 2 or not n % 5:
        return -1
    x, mods = 1, set()
    while x not in mods:
        mods.add(x)
        x = 10 * x % n
    return len(mods)

lechevalier 所用的这个方法的思路，正是我上面说的，只是并非暴力循环，而是不断迭代。我的疑问是，为何一定能保证，mods 长度刚好是循环的位数？

方法类似这里给出的答案：How to Calculate Recurring Digits?

You can calculate the decimal representation of a / b using the long-division algorithm you learned at school, as Mark Ransom said. To calculate each successive digit, divide the current dividend (numerator or remainder) by b, and find the next dividend as the remainder multiplied by 10 (“bringing down a 0”). When a remainder is the same as some previous remainder, it means that the digits from then on will repeat as well, so you can note this fact and stop.

明白了。其实整个迭代的过程就是去做一次 long division。long division 就是我们小学学过的那种除法计算。


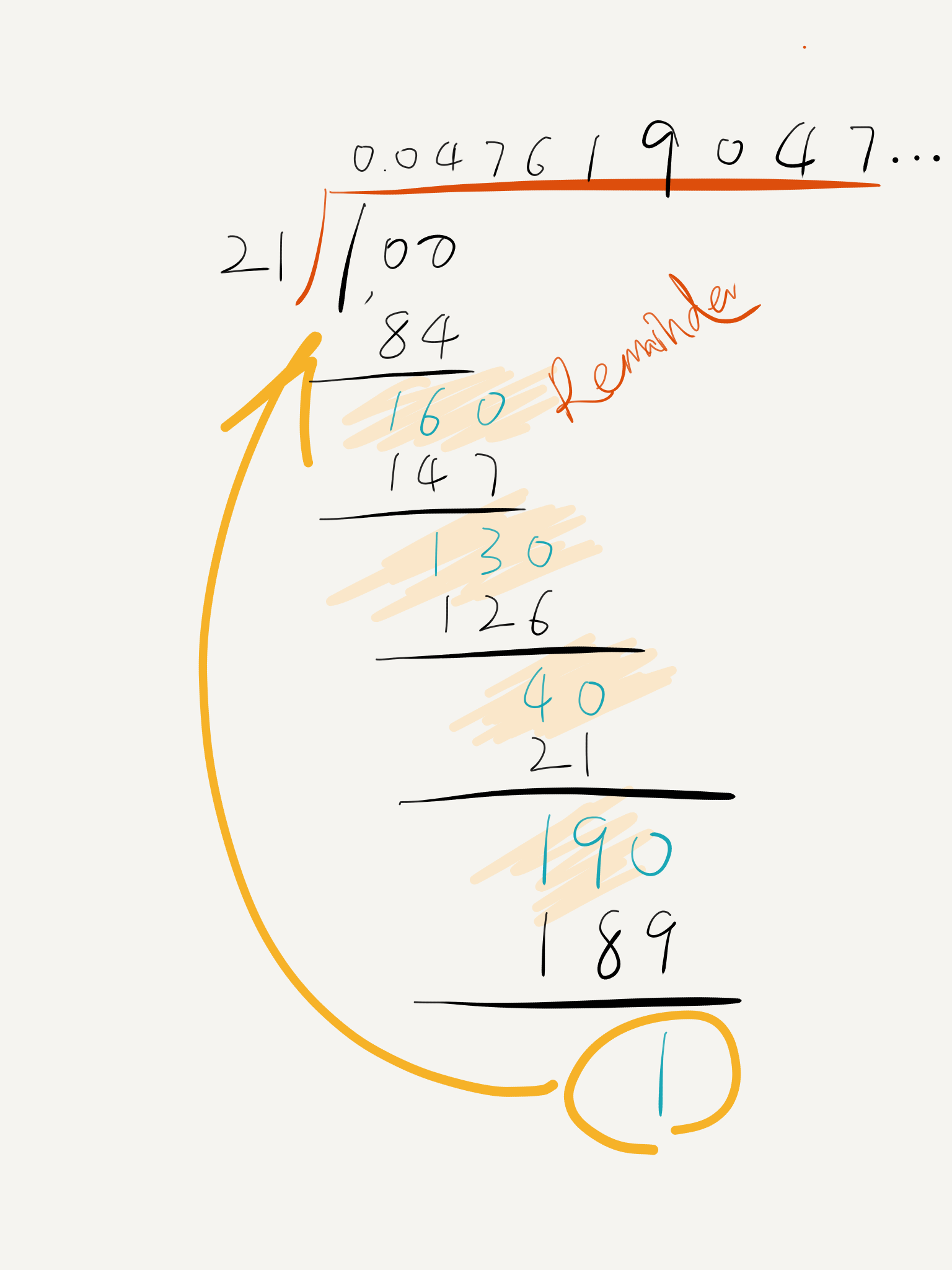
那么为什么这样一种循环就比之前我想的那种暴力破解快呢？答案就在于迭代。每次只用 remainder 乘 10 进行迭代，一个非常小的数，算起来自然比用 $10^{n}$ 直接去除要快得多。

参考文章：

• Calculating Euler’s totient function values.
• How to Calculate Recurring Digits?